Differentiation rules

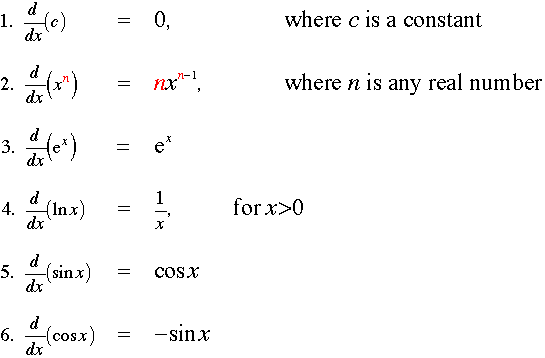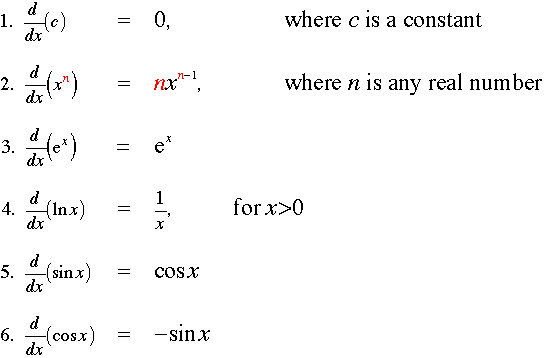
Elementary rules of differentiation

Unless otherwise stated, all functions are functions of real numbers that return real values; although more generally, the formulae below apply wherever they are well defined—including complex numbers.

Differentiation is linear

For any functions f and g and any real numbers a and b the derivative of the function h = af + bg with respect to x is

In Leibniz's notation this is written as:

Special cases include:

The constant factor rule

The sum rule

The subtraction rule

The product rule

For the functions f and g, the derivative of the function h = f g with respect to x is

In Leibniz's notation this is written

The chain rule

The derivative of the function of a function h = f) with respect to x is

In Leibniz's notation this is written as:

However, by relaxing the interpretation of h as a function, this is often simply written

The inverse function rule

If the function f has an inverse function g, meaning that g) = x and f) = y, then

In Leibniz notation, this is written as

Power laws, polynomials, quotients, and reciprocals

The polynomial or elementary power rule

If, for any number then

Special cases include:

Constant rule: if then f is the constant function f = c, for some number c, and, for all x, f′ = 0.
if f = x, then f′ = 1. This special case may be generalized to: The derivative of an affine function is constant: if f = ax + b, then f′ = a.

Combining this rule with the linearity of the derivative and the addition rule permits the computation of the derivative of any polynomial.

The reciprocal rule

The derivative of h = 1/f for any function f is:

In Leibniz's notation, this is written

The reciprocal rule can be derived from the chain rule and the power rule.

The quotient rule

If f and g are functions, then:

wherever g is nonzero.

This can be derived from reciprocal rule and the product rule. Conversely the reciprocal rule may be derived from the special case f = 1.

Generalized power rule

The elementary power rule generalizes considerably. The most general power rule is the functional power rule: for any functions f and g,

wherever both sides are well defined.

Special cases:

If f = xa, f′ = axa − 1 when a is any real number and x is positive.
The reciprocal rule may be derived as the special case where g = −1.

Derivatives of exponential and logarithmic functions

note that the equation above is true for all c, but the derivative for c < 0 yields a complex number.

the equation above is also true for all c but yields a complex number if c<0.

Logarithmic derivatives

The logarithmic derivative is another way of stating the rule for differentiating the logarithm of a function :

wherever f is positive.

Derivatives of trigonometric functions

It is common to additionally define an inverse tangent function with two arguments,. Its value lies in the range and reflects the quadrant of the point. For the first and fourth quadrant one has. Its partial derivatives are

Derivatives of hyperbolic functions

Derivatives of special functions

Derivatives of integrals

Suppose that it is required to differentiate with respect to x the function

where the functions and are both continuous in both and in some region of the plane, including , and the functions and are both continuous and both have continuous derivatives for. Then for :

This formula is the general form of the Leibniz integral rule and can be derived using the fundamental theorem of calculus.